En 1736, el matemático Leonhard Euler (1707–1783) se interesó por un problema que hacía referencia a los siete puentes que permitían visitar los distritos de la ciudad de Königsberg (‘Montaña del Rey’, en alemán). En aquella época la ciudad de Königsberg aún existía. Estaba construida a orillas del río Pregel sobre dos islas que se encontraban en el centro de la corriente del río. Por muchos siglos Königsberg perteneció a Prusia, corazón de la Alemania imperial; sin embargo, al finalizar la II Guerra Mundial, Prusia fue literalmente destrozada y arrasada por los soviéticos;  los soviéticos construyeron una ciudad nueva sobre las ruinas de Königsberg llamada Kaliningrado.

El problema de los siete puentes de Königsberg

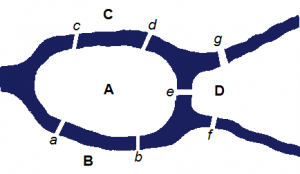
En la Figura 1. se muestran los distritos de la ciudad de Königsberg como A, B, C y D y los puentes como a, b, c, d, e, f y g. La pregunta que se hacían en aquella época los ciudadanos de Königsberg era ¿es posible hacer una caminata que inicie en cualquier punto de la ciudad, cruzando cada puente exactamente una vez y regresando al punto de partida? (Si no había visto éste problema antes, considere dedicarle un momento para buscar la respuesta por su cuenta. Informalmente no es difícil llegar a la conclusión que el camino propuesto en el planteamiento del problema no existe, sin embargo, probar esto formalmente es más difícil.)

Intentemos encontrar el recorrido circular solicitado, comenzando -por ejemplo- en A. La primera vez, cuando regresemos a A,  hemos utilizado dos de los cinco puentes conectados con A. La siguiente vez que regresemos a A hemos utilizado cuatro puentes. En este momento debemos abandonar A utilizando el quinto puente, pero ya no existe posibilidad de regresar al punto A sin utilizar uno de los cinco puentes por segunda vez. Esto permite ver que el problema planteado para los puentes de la ciudad de Königsberg no tiene solución. Utilizando un análisis similar, se puede ver que también es imposible encontrar algún recorrido, no necesariamente circular (un recorrido que puede terminar en un punto diferente al que se inició), que utilice cada puente sólo una vez.

Leonhard Euler y el nacimiento de la teoría de grafos

Lo que Euler hizo con base en el problema de los siete puentes de Königsberg iba más allá de solucionar el popular problema. Su artículo, titulado Solutio problematis ad geometriam situs pertinentis (Sobre la solución de un problema relacionado con la geometría de posición) de algún modo marcó el nacimiento de lo que hoy llamamos teoría de grafos, una rama de las matemáticas discretas que en los últimos tres siglos se ha convertido en el principal lenguaje matemático para describir las propiedades de las redes en general.

Después de describir el popular problema de los puentes, Euler presentó su trabajo con las siguientes palabras (aproximadamente): Con base en el planteamiento expuesto, formulo el siguiente problema general: dada cualquier configuración del río y las ramificaciones en las que pueda dividirse y cualquier cantidad de puentes, determinar si es o no posible cruzar cada puente exactamente una vez. Euler se dió cuenta que la forma exacta de las orillas o de las islas no era importante, la solución al problema dependía sólo de las propiedades de la conexión entre los distritos.

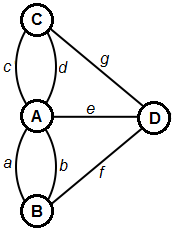
La solución que se presenta en la actualidad, que quizá ahora pueda parecer sencilla, no era obvia en el siglo XVIII pues utiliza un grafo. Un grafo es un objeto matemático que consta de un conjunto de nodos (llamados también puntos o vértices) y un conjunto de arcos que muestran la relación entre los nodos (los arcos también reciben el nombre de líneas, enlaces o aristas). La Figura 2. muestra un grafo que representa el problema de los puentes de Königsberg. Utiliza cuatro nodos representando los distritos y siete arcos que representan los puentes que los interconectan (este tipo de gráfico nunca lo utilizó Euler).

Grado, camino, sendero, trayecto, ciclo y otros conceptos

[La terminología de la teoría de grafos aún no es universal, por esto los nombres presentados a continuación pueden ser diferentes a los que usted ya conoce para el mismo concepto.]

El número de arcos que “tocan” un nodo es llamado el grado del nodo. Por ejemplo, en el grafo de Königsberg, el nodo A tiene grado cinco, pues cinco arcos -cinco puentes- tocan dicho nodo.

Dependiendo de la forma en que se recorra un grafo, la secuencia de arcos y nodos visitados recibe un nombre diferente. Puede ser un camino (walk), un camino cerrado (closed walk), un sendero (trail), un sendero cerrado (closed trail), un trayecto (path) o un ciclo (cycle).

• Camino: Si se sigue una secuencia de arcos en un grafo que permiten visitar los nodos sin importar dónde se inició el paseo y donde terminó o si se dejó de visitar algún nodo o algún arco o si se pasó varias veces por el mismo nodo o arco, la secuencia recibe el nombre de camino (walk).
• Camino cerrado: Si se sigue una secuencia de arcos en un grafo que permiten visitar los nodos garantizando que el paseo inicia y termina en el mismo nodo, pero sin importar si se dejó de visitar algún nodo o algún arco o si se pasó varias veces por el mismo nodo o arco, la secuencia recibe el nombre de camino cerrado (closed walk).
• Sendero: Si se sigue una secuencia de arcos en un grafo que permiten visitar los nodos sin importar dónde se inició el paseo y donde terminó o si se dejó de visitar algún nodo o si se pasó varias veces por el mismo nodo, pero se garantiza que cada arco se visita una sola vez, la secuencia recibe el nombre de sendero (trail).
• Sendero cerrado: Si se sigue una secuencia de arcos en un grafo que permiten visitar los nodos garantizando que el paseo inicia y termina en el mismo nodo y que cada arco se visita una sola vez, pero sin importar si se dejó de visitar algún nodo o si se pasó varias veces por el mismo nodo, la secuencia recibe el nombre de sendero cerrado (closed trail).
• Trayecto: es un sendero (secuencia de arcos diferentes sin importar dónde se inició el paseo y donde terminó) que visita cada nodo solamente una vez.
• Ciclo: En un grafo con tres o más nodos, un ciclo es un sendero cerrado (secuencia de arcos diferentes garantizando que el paseo inicia y termina en el mismo nodo) que visita cada nodo solamente una vez.

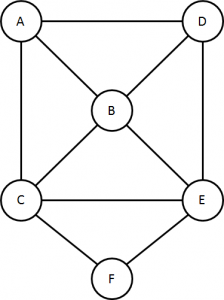
Por ejemplo, en la figura 3, si se visitan los nodos (A, B, C, E, B, C) el recorrido es un camino (walk), pero no es un sendero (trail) ya que el arco que interconecta B con C se visita dos veces. Si se visitan los nodos (A, B, C, E, B, D) el recorrido hecho es un sendero (trail) pues cada arco del recorrido se visita sólo una vez pero no es un trayecto (path) ya que el nodo B se visita más de una vez.  Si se recorren los nodos (A,B,C,E,B,D,A) se tiene un sendero cerrado (closed trail) pues inicia y termina en el mismo nodo pero no se tiene un ciclo (cycle) ya que el nodo B se visita más de una vez. Finalmente, el recorrido (A, B, C, F, E, D, A) es un ciclo (cycle).

Un sendero de Euler pasa por todos los nodos visitando cada arco una sola vez y un tour de Euler es un sendero de Euler que además de pasar por todos los nodos visitando cada arco una sola vez, inicia y termina en el mismo nodo. Estos dos conceptos fueron estudiados por Euler al resolver el problema de los puentes de Königsberg (aunque él no utilizó esos nombres para los conceptos).

La solución de Euler

Ahora, el problema planteado podemos enunciarlo como:

Dado un grafo, ¿es posible determinar si tiene un sendero cerrado? Es decir, dado un grafo cualquiera ¿Es posible determinar si el grafo se puede recorrer iniciando y terminando en el mismo nodo visitando cada arco exactamente una vez?

Euler probó que una condición necesaria para la existencia del tour de Euler es que todos los nodos en el grafo sean de grado par, y estableció -sin prueba- que un grafo cuyos nodos sean de grado par tendrá un tour de Euler. La primera prueba completa de esta última afirmación -realizada por Carl Hierholzer- fue publicada hasta 1873.

Para garantizar la existencia de senderos de Euler, máximo dos nodos pueden tener grado impar (los demás deben ser de grado par). Si todos los nodos son de grado par y no hay nodos de grado impar, todos los senderos de Euler son tour de Euler. Si hay exactamente dos nodos de grado impar, los posibles senderos inician en uno de ellos y terminan en el otro. En ocasiones un grafo que tiene un sendero de Euler pero no tienen un tour de Euler es llamado semi-Euleriano.

El problema de la existencia de los senderos de Euler y de los tour de Euler en las redes -al igual que el problema relacionado de los trayectos Hamiltonianos y los ciclos Hamiltonianos (trayectos que visitan cada nodo exactamente una vez)- son aún de gran interés para los matemáticos.

El artículo de Euler de 1736 (que realmente fue publicado hasta 1741) sobre el problema de los puentes de Königsberg es visto como la primera gran contribución a la teoría de grafos -aunque la solución de Euler nunca menciona los grafos-. El artículo The Truth about Königsberg de Brian Hopkins y Robin J. Wilson presenta el contexto histórico de la solución de Euler, muestra el método de solución utilizado, describe la “geometría de posición” y hace un breve seguimiento hasta la actualidad.

La teoría de grafos y el estudio de las redes

En su forma más simple, una red no es más que un conjunto de elementos discretos (los nodos) y un conjunto de conexiones (los arcos) que enlazan los elementos. Los elementos y sus conexiones pueden ser cualquier cosa – personas y sus vínculos de amistad, computadores y sus enlaces de comunicaciones, páginas web y sus hiper-enlaces, compuestos químicos y sus reacciones, artículos científicos y sus citas por otros autores, etcétera.

La teoría de grafos es muy poderosa, pues al abstraer los detalles de un problema es capaz de describir importantes características topológicas con una claridad que sería imposible si se conservaran todos los detalles del problema. Esta teoría, nacida a partir del problema de los sietes puentes de la ciudad de Königsberg, es muy importante en el estudio de la redes y, en consecuencia, para todas las personas interesadas en este tema.

Referencias

Newman, Barabási, Watts. The Structure and Dynamics of Networks. 2006. Princeton University Press.

Jungnickel, D.  Graphs, Networks and Algorithms. 2007. Springer-Verlag.

Luccio, Pagli, Steel. Mathematical and Algorithmic Foundations of the Internet. 2011. CRC Press